人の可能性を現実にする、シンプルな方法
探求について探求しながら、対象を探求する
私たち人類にとって「学習」は特別な意味を持ちます。
例えば、
- 学習 = 人生
- 学習 = 自己実現
- 学習 = 仕事の道具を手にいれること
- 学習 = 仕事そのもの
- 学習 = 家事
人生のあらゆる場面が「学習」です。
人格における絶え間ざる学習を孔子は「道」と説きました。私たち日本人が慣れ親しんでいる禅文化は、道元禅師によって、中国大陸、朝鮮半島の土着の宗教が削ぎ落とされ、同じく「絶え間ない改善文化」を支える「道」となりました。
そして、豊田佐吉と大野耐一に起源を持つ生産性のたゆまぬ向上を表し、世界中の製造現場に広がり、さらにはソフトウェア開発に広がった「カイゼン」も、「絶え間ない学習」です。
絶え間ない学習とは何か?
では、この「絶え間なく続く学習」とは何か、いかなる構造をしているか?を私たちは、言葉にすることによって、「体系化」する必要があります。
カンセイ(これも世界にでた言葉ですね、確かカントが最初に使ったらしいですが)の問題にしておくことはできません。
カンセイで理解することを強要するならば、
- 経験
- センス
- 生まれ持った人格
に頼ることになります。これでは、一部の幸運な人だけの特権になってしまいます。
つまり、私たちが飛躍的な前進を遂げるには、「特別だったことを、当たり前にする」時です。
そのためには「学べるもの」として、「継続的改善」「継続的な学習」とは何か?を言葉にすること、つまり体系化が必要です。
入れ子構造
継続的カイゼンや、継続的な学習(高いレベルの)が、カンセイや経験に頼ってきた理由は、「言葉の限界」にあります。
言語や論理は、「入れ子構造」を持つ動的なものを、うまく表すことができません。デイビッドボームは内臓秩序として、言語化を試みたのがそれです。また数学の世界、複雑系の世界で知られる、シンプルな漸化式は、まさに「入れ子構造」で「動的な存在」です。
式自体は、シンプルですが、そこに数字を入れ現実世界にマッピングしたとき、複雑な挙動を示します。
高次の学習の定義も、これに非常によく似ています。
つまり「言葉として表しても、捉えづらい」ということです。
しかし、あえて言葉にすると、
探求について探求しながら、対象を探求する
このような構造を作り出すことが、継続的カイゼンであり、高次の継続学習になります。
言葉ではなく、体験を通して学ぶ
ところで、先の漸化式も「式を眺めているだけ」では、何もわかりません。体験、つまり我々の住んでいる「実次元」、時間軸の中におけば、よくわかります。
例えば、以下の漸化式をみて、どんなグラフが生まれるか?を想像しようとしても、考えられるものではありません。
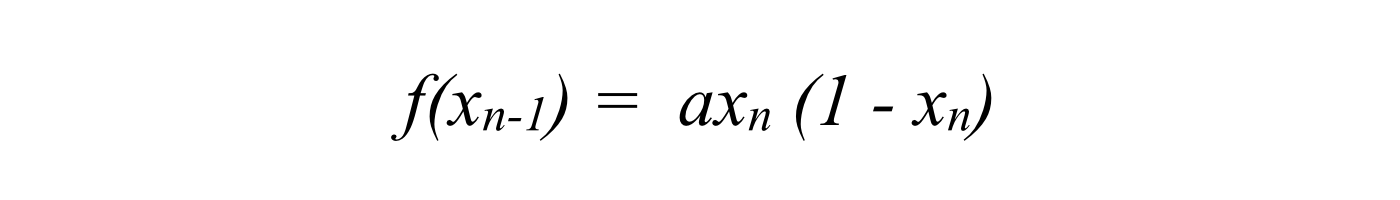
ロジスティック写像の式(aは定数0
実際に、スプレッドシートなどに展開して、簡単な実験を行うと「パラメータaによって、かなり違うグラフ」になることが確認できます。全て同じ、シンプルな式ですが、初期値や a の値が違うと、グラフが大きく変わります。
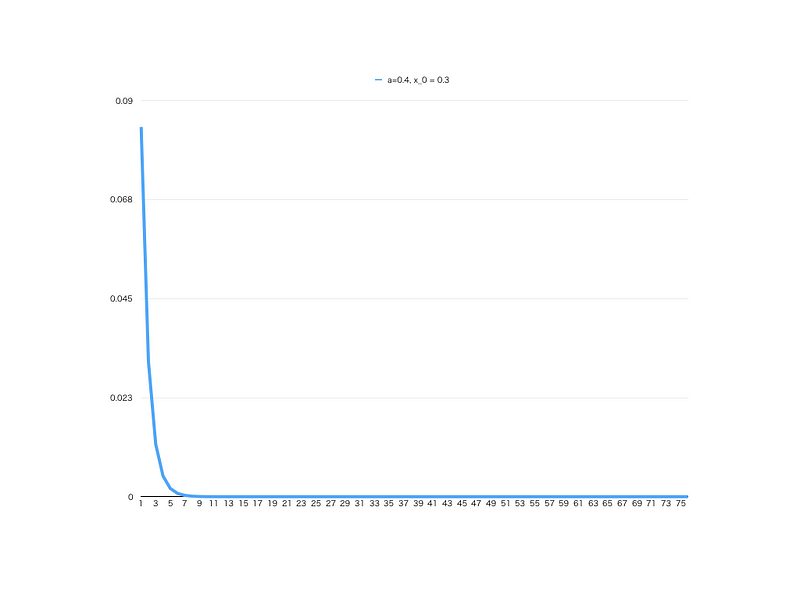
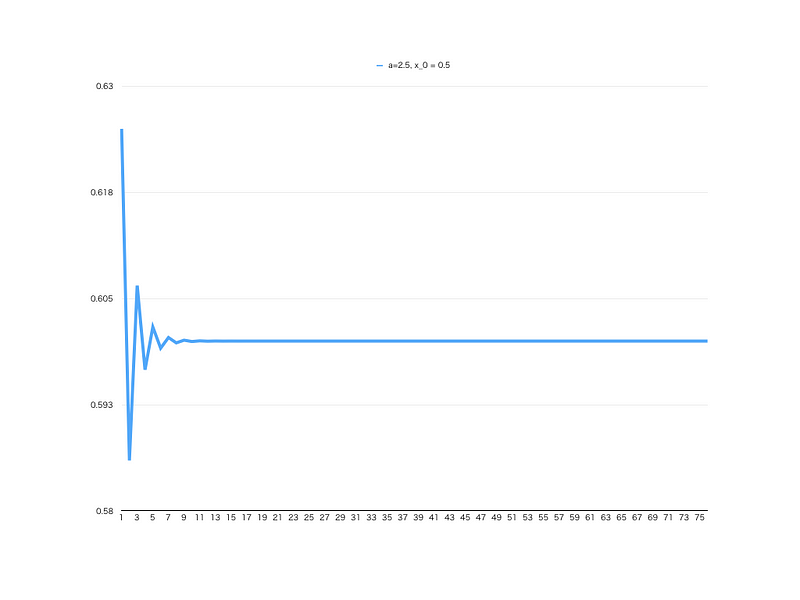
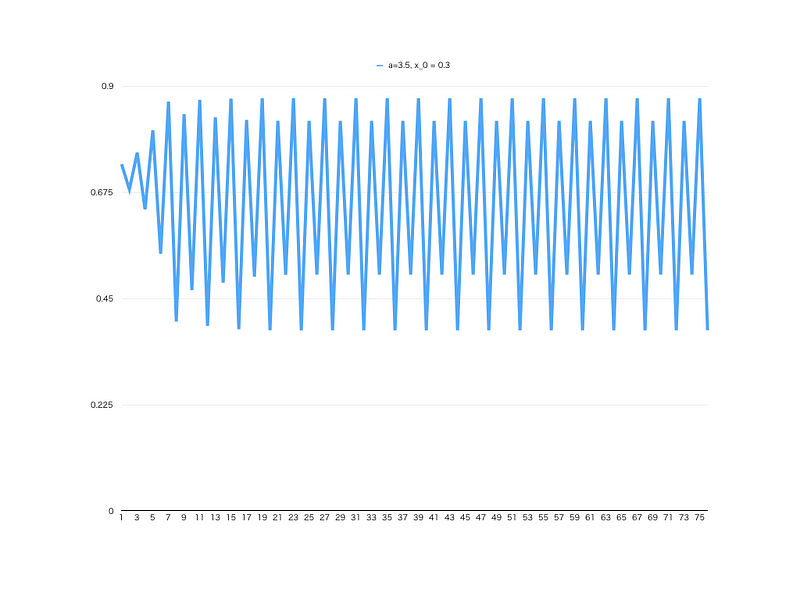
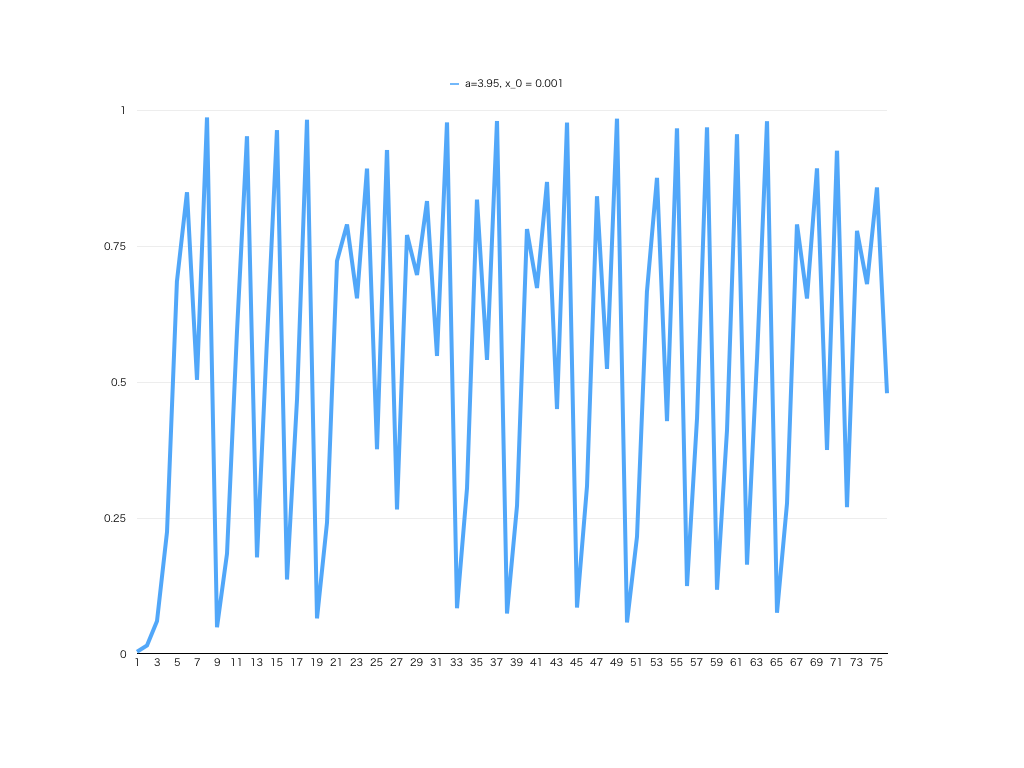
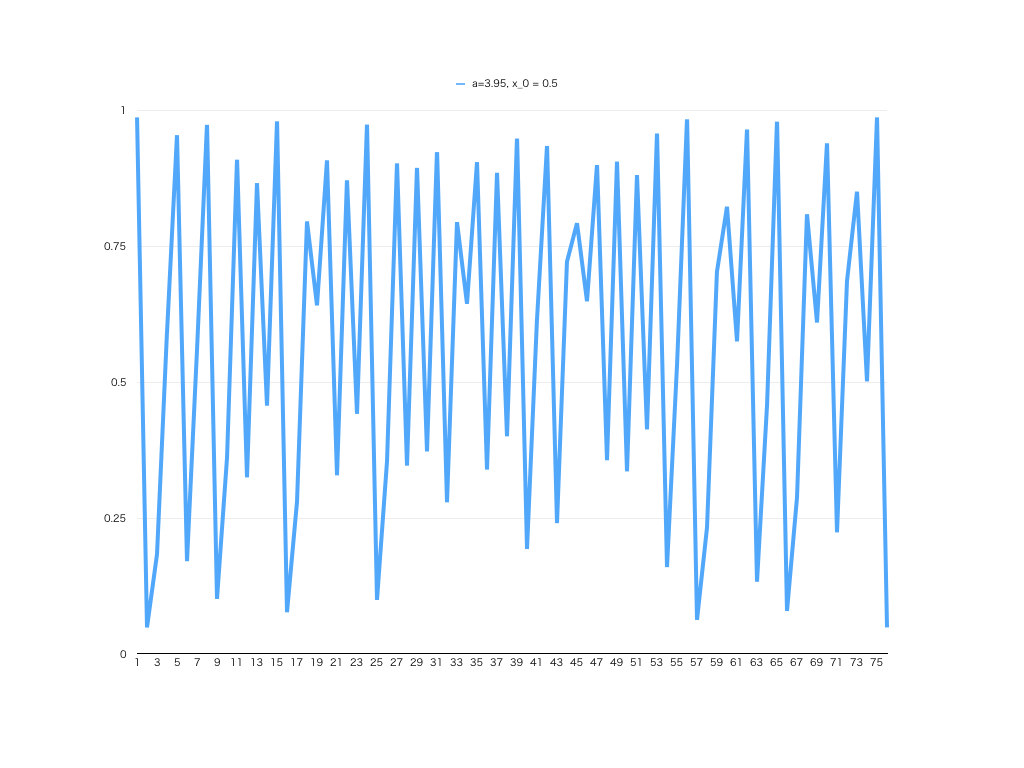
なお、このロジスティック写像と呼ばれる数式は、次元数や周期性などから分析され、違う視点から見れば「明確な構造」があることが見て取れます。
同様に、「探求について探求しながら、対象を探求する」も、具体的な行動を見れば、明らかになります。
アクティブラーニングの秘訣
最近、学校教育の世界では、「アクティブラーニング」なるものが流行っているというより、教育現場にいる先生方に求めるようになりました。
そのような経緯もあって、成功事例の記事もあれば、現場には重荷だという批判記事も出始めています。
しかし、「探求について探求しながら、対象を探求する」の構造を明らかにし、理解することができれば(簡単です)、大きなヒントになるはずです。
具体的には、以下のようなステップを取ります。特に大人の場合に有効ですが、子供たちに対しては、数日どころか、年間を通して、このような行動をとれば、自然と「自発的に学習」します。しかも、「継続的なカイゼン」を行いながら。
ステップは以下の通りです。
- 特定の議論する課題をあげる(例えば、良い学習者とは?)
- 期待する結果をあげる(議論の結果、どんな結果を得たいか?)
- 議論をスタートさせる
- 【重要】途中で止める
- 【重要】ここまでの議論は、どうだったか?を振り返る
- 【重要】期待する結果は、修正しなくてよいか?を考える
- 【重要】この後の議論は、どうするとよいか?を考える
- 再び、議論を開始
- 結論を出す
- 【重要】結果を確認し、議論スタートと、途中からの議論を振り返り、学びを引き出す
このように、議論の途中に議論について議論し、最終的な結果を得た時にも、議論の流れを振り返るという構造を作ることで、
- 質の高い継続学習のフラクタル構造
が出来上がります。これを、意識的にずっと行っていくことが、私たち toiee Lab がさす「自ら学ぶこと」として定義しています。
単純に「自発的」と呼ぶだけでは、大した進歩はしていません。このようなフラクタル構造を持った学習は、漸化式のように「現在の値」が「次の値を作る」が継続し続ける構造をもつため、必然として「自発的」であり、「継続的」になります。
なぜ、こんな駄文を書いたのか?
ここまで書いて、私はこの文章は「駄文だ」と思っています。読者を非常に限定しているし、前提知識が山ほど必要とします。
でも、「研究所っぽい記事」を載せておいてほしい、紹介した時に「権威」を感じた方がいいという意見があったので、書いてみました。
書きながら、一休和尚のエピソードを思い出しました。
あるとき、権力者から「お経を唱えてほしい」と頼まれ、乞食の格好をして訪問したところ、追い出されました。次の日、高価な袈裟を着て、身なりを整えて、再び訪問しました。
すると、すんなり通されましたが、一休和尚は奥の祭壇には上がらず、玄関で立ち止まり「ここで結構」と言います。そして「昨日の乞食は自分であり、この体は同じだから上がれない」と伝え、法衣を手渡し、「これを祭壇に祀って祈りなさい」と伝えました。
toiee Lab のことを好きになってくれて、紹介を考えてくれる方々がいらっしゃいますが、「権威」や「目立つ実績」を用意してほしいと言われます。
確かに必要だと思いますが、それらは結果だと思います。それを作って、人に訴えるというのは、「法衣を拝む」行為に近いと、自分を戒めた次第です。
今後は、こんな駄文よりは、もっとわかりやすく、楽しく、具体事例をお届けしたいと思います。
とはいえ、上記は権威めいた書き方をしましたが、以上で述べたことは「誰もが理解できる」ことです。
鍵は「やってみること」です。
何事も、実践あるのみです。
実践をするための方法や、実例を紹介していきますので、お楽しみに。
追伸:
研究者としては実践だけでなく、詳細な論理構造の構築に努めています。上記のような論理は権威のためではなく、必要だと思って考えています。つまり、フラクタル構造は、「高次学習には欠かせません」。
上記の記事で現れた数々の分野は、深く関係しています。もし、あなたが「学習とは何か?」を、学術的に探求したいなら、出てきた用語、分野などを調べてください。すごく役立つはずです。
そのうち、「売れない本」で、細かく全てを描いてみたいと思っています。